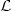Let $\mathcal{L}$ 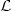 be a language.A balanced pair (u,v) consists of two words u and v in $\mathcal{L}$
be a language.A balanced pair (u,v) consists of two words u and v in $\mathcal{L}$ 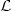 which have the same number ofoccurrences of each letter.It is irreducible if the pairs of strict prefixes of u and v of the same length do not form balanced pairs. In this article, we are interested in computing the set of irreducible balanced pairs on several cases of languages.We make connections with the balanced pairs algorithm and discrete geometrical constructions related to substitutive languages.We characterize substitutive languages which have infinitely many irreducible balanced pairs of a given form.
which have the same number ofoccurrences of each letter.It is irreducible if the pairs of strict prefixes of u and v of the same length do not form balanced pairs. In this article, we are interested in computing the set of irreducible balanced pairs on several cases of languages.We make connections with the balanced pairs algorithm and discrete geometrical constructions related to substitutive languages.We characterize substitutive languages which have infinitely many irreducible balanced pairs of a given form.