We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We give strengthened versions of the Herwig–Lascar and Hodkinson–Otto extension theorems for partial automorphisms of finite structures. Such strengthenings yield several combinatorial and group-theoretic consequences for homogeneous structures. For instance, we establish a coherent form of the extension property for partial automorphisms for certain Fraïssé classes. We deduce from these results that the isometry group of the rational Urysohn space, the automorphism group of the Fraïssé limit of any Fraïssé class that is the class of all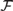 
${\cal F}$-free structures (in the Herwig–Lascar sense), and the automorphism group of any free homogeneous structure over a finite relational language all contain a dense locally finite subgroup. We also show that any free homogeneous structure admits ample generics.
