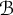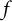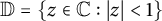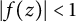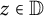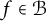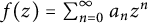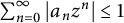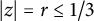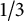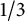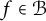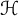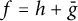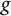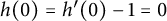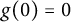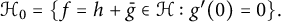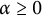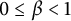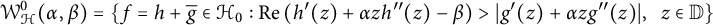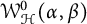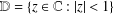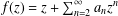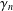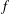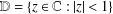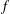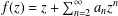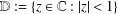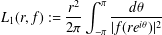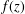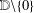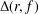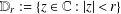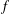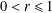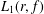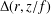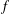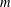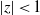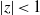14 results
Bohr–Rogosinski radius for a certain class of close-to-convex harmonic mappings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 31 January 2023, pp. 1014-1029
- Print publication:
- September 2023
-
- Article
- Export citation
Cognitive miserliness in argument literacy? Effects of intuitive andanalytic thinking on recognizing fallacies
-
- Journal:
- Judgment and Decision Making / Volume 17 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 01 January 2023, pp. 331-361
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chapter 2 - Immunohistochemistry Quality Assurance and Quality Control
-
-
- Book:
- Immunohistochemistry
- Published online:
- 16 June 2022
- Print publication:
- 07 July 2022, pp 24-66
-
- Chapter
- Export citation
Chapter 5 - Distraction and Heart of Darkness, Lord Jim, The Secret Agent and Under Western Eyes
- from Part II - Published Texts
-
- Book:
- Conrad's Decentered Fiction
- Published online:
- 10 March 2022
- Print publication:
- 17 March 2022, pp 94-114
-
- Chapter
- Export citation

Aspects of Truth
- A New Religious Metaphysics
-
- Published online:
- 06 October 2020
- Print publication:
- 22 October 2020
Chapter 7 - Analyticity
- from Part II - Applications
-
- Book:
- A Theory of Truthmaking
- Published online:
- 18 April 2020
- Print publication:
- 30 April 2020, pp 136-149
-
- Chapter
- Export citation
1 - Introduction
-
- Book:
- The Attending Mind
- Published online:
- 14 February 2020
- Print publication:
- 05 March 2020, pp 1-5
-
- Chapter
- Export citation
4 - Proposing a New Type of Definition
- from Part II - The Nature of Trust
-
- Book:
- Trust in Medicine
- Published online:
- 19 August 2019
- Print publication:
- 22 August 2019, pp 31-38
-
- Chapter
- Export citation
ON SOME SUBCLASSES OF HARMONIC MAPPINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 10 July 2019, pp. 130-140
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
ON OZAKI CLOSE-TO-CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 20 September 2018, pp. 89-100
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
LOGARITHMIC COEFFICIENTS OF SOME CLOSE-TO-CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 228-237
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
INTEGRAL MEANS AND DIRICHLET INTEGRAL FOR CERTAIN CLASSES OF ANALYTIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 16 July 2015, pp. 315-333
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
REMARKS ON THE UNIVALENCE CRITERION OF PASCU AND PASCU
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 22 August 2013, pp. 210-216
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
Explicit criteria for several types of ergodicity of the embedded M/G/1 and GI/M/n queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 778-790
- Print publication:
- September 2004
-
- Article
- Export citation