In a singularly perturbed limit, we analyse the existence and linear stability of steady-state hotspot solutions for an extension of the 1-D three-component reaction-diffusion (RD) system formulated and studied numerically in Jones et. al. [Math. Models. Meth. Appl. Sci., 20, Suppl., (2010)], which models urban crime with police intervention. In our extended RD model, the field variables are the attractiveness field for burglary, the criminal population density and the police population density. Our model includes a scalar parameter that determines the strength of the police drift towards maxima of the attractiveness field. For a special choice of this parameter, we recover the ‘cops-on-the-dots’ policing strategy of Jones et. al., where the police mimic the drift of the criminals towards maxima of the attractiveness field. For our extended model, the method of matched asymptotic expansions is used to construct 1-D steady-state hotspot patterns as well as to derive nonlocal eigenvalue problems (NLEPs) that characterise the linear stability of these hotspot steady states to 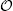${\cal O}$(1) timescale instabilities. For a cops-on-the-dots policing strategy, we prove that a multi-hotspot steady state is linearly stable to synchronous perturbations of the hotspot amplitudes. Alternatively, for asynchronous perturbations of the hotspot amplitudes, a hybrid analytical–numerical method is used to construct linear stability phase diagrams in the police vs. criminal diffusivity parameter space. In one particular region of these phase diagrams, the hotspot steady states are shown to be unstable to asynchronous oscillatory instabilities in the hotspot amplitudes that arise from a Hopf bifurcation. Within the context of our model, this provides a parameter range where the effect of a cops-on-the-dots policing strategy is to only displace crime temporally between neighbouring spatial regions. Our hybrid approach to study the NLEPs combines rigorous spectral results with a numerical parameterisation of any Hopf bifurcation threshold. For the cops-on-the-dots policing strategy, our linear stability predictions for steady-state hotspot patterns are confirmed from full numerical PDE simulations of the three-component RD system.

In a one-dimensional domain, the stability of localized spike patterns is analysed for two closely related singularly perturbed reaction–diffusion (RD) systems with Brusselator kinetics. For the first system, where there is no influx of the inhibitor on the domain boundary, asymptotic analysis is used to derive a non-local eigenvalue problem (NLEP), whose spectrum determines the linear stability of a multi-spike steady-state solution. Similar to previous NLEP stability analyses of spike patterns for other RD systems, such as the Gierer–Meinhardt and Gray–Scott models, a multi-spike steady-state solution can become unstable to either a competition or an oscillatory instability depending on the parameter regime. An explicit result for the threshold value for the initiation of a competition instability, which triggers the annihilation of spikes in a multi-spike pattern, is derived. Alternatively, in the parameter regime when a Hopf bifurcation occurs, it is shown from a numerical study of the NLEP that an asynchronous, rather than synchronous, oscillatory instability of the spike amplitudes can be the dominant instability. The existence of robust asynchronous temporal oscillations of the spike amplitudes has not been predicted from NLEP stability studies of other RD systems. For the second system, where there is an influx of inhibitor from the domain boundaries, an NLEP stability analysis of a quasi-steady-state two-spike pattern reveals the possibility of dynamic bifurcations leading to either a competition or an oscillatory instability of the spike amplitudes depending on the parameter regime. It is shown that the novel asynchronous oscillatory instability mode can again be the dominant instability. For both Brusselator systems, the detailed stability results from NLEP theory are confirmed by rather extensive numerical computations of the full partial differential equations system.