1 results
Residual torsion-free nilpotence, bi-orderability, and two-bridge links
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 25 January 2023, pp. 394-457
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
-
Residual torsion-free nilpotence has proved to be an important property for knot groups with applications to bi-orderability and ribbon concordance. Mayland proposed a strategy to show that a two-bridge knot group has a commutator subgroup which is a union of an ascending chain of para-free groups. This paper proves Mayland’s assertion and expands the result to the subgroups of two-bridge link groups that correspond to the kernels of maps to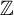
$\mathbb{Z}$. We call these kernels the Alexander subgroups of the links. As a result, we show the bi-orderability of a large family of two-bridge link groups. This proof makes use of a modified version of a graph-theoretic construction of Hirasawa and Murasugi in order to understand the structure of the Alexander subgroup for a two-bridge link group.
