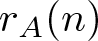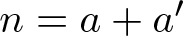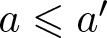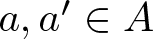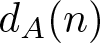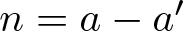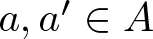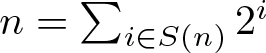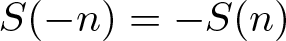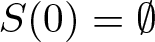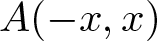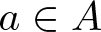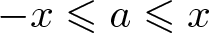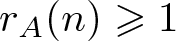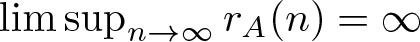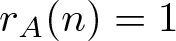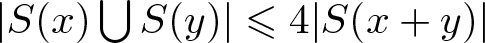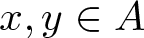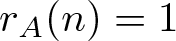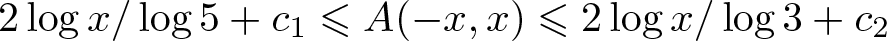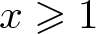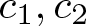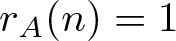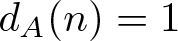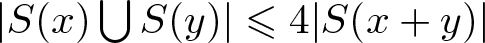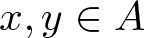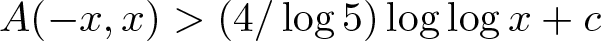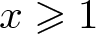For a nonempty set A of integers and an integer n, let 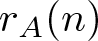 $r_{A}(n)$ be the number of representations of n in the form
$r_{A}(n)$ be the number of representations of n in the form 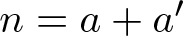 $n=a+a'$, where
$n=a+a'$, where 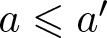 $a\leqslant a'$ and
$a\leqslant a'$ and 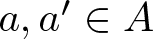 $a, a'\in A$, and
$a, a'\in A$, and 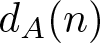 $d_{A}(n)$ be the number of representations of n in the form
$d_{A}(n)$ be the number of representations of n in the form 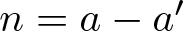 $n=a-a'$, where
$n=a-a'$, where 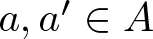 $a, a'\in A$. The binary support of a positive integer n is defined as the subset S(n) of nonnegative integers consisting of the exponents in the binary expansion of n, i.e.,
$a, a'\in A$. The binary support of a positive integer n is defined as the subset S(n) of nonnegative integers consisting of the exponents in the binary expansion of n, i.e., 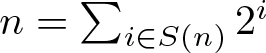 $n=\sum_{i\in S(n)} 2^i$,
$n=\sum_{i\in S(n)} 2^i$, 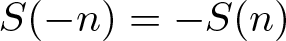 $S(-n)=-S(n)$ and
$S(-n)=-S(n)$ and 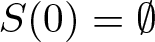 $S(0)=\emptyset$. For real number x, let
$S(0)=\emptyset$. For real number x, let 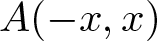 $A(-x,x)$ be the number of elements
$A(-x,x)$ be the number of elements 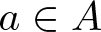 $a\in A$ with
$a\in A$ with 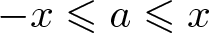 $-x\leqslant a\leqslant x$. The famous Erdős-Turán Conjecture states that if A is a set of positive integers such that
$-x\leqslant a\leqslant x$. The famous Erdős-Turán Conjecture states that if A is a set of positive integers such that 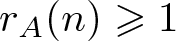 $r_A(n)\geqslant 1$ for all sufficiently large n, then
$r_A(n)\geqslant 1$ for all sufficiently large n, then 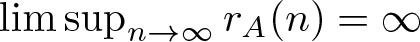 $\limsup_{n\rightarrow\infty}r_A(n)=\infty$. In 2004, Nešetřil and Serra initially introduced the notation of “bounded” property and confirmed the Erdős-Turán conjecture for a class of bounded bases. They also proved that, there exists a set A of integers satisfying
$\limsup_{n\rightarrow\infty}r_A(n)=\infty$. In 2004, Nešetřil and Serra initially introduced the notation of “bounded” property and confirmed the Erdős-Turán conjecture for a class of bounded bases. They also proved that, there exists a set A of integers satisfying 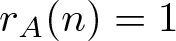 $r_A(n)=1$ for all integers n and
$r_A(n)=1$ for all integers n and 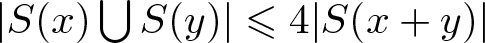 $|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for
$|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for 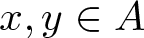 $x,y\in A$. On the other hand, Nathanson proved that there exists a set A of integers such that
$x,y\in A$. On the other hand, Nathanson proved that there exists a set A of integers such that 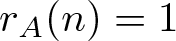 $r_A(n)=1$ for all integers n and
$r_A(n)=1$ for all integers n and 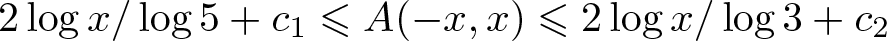 $2\log x/\log 5+c_1\leqslant A(-x,x)\leqslant 2\log x/\log 3+c_2$ for all
$2\log x/\log 5+c_1\leqslant A(-x,x)\leqslant 2\log x/\log 3+c_2$ for all 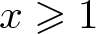 $x\geqslant 1$, where
$x\geqslant 1$, where 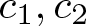 $c_1,c_2$ are absolute constants. In this paper, following these results, we prove that, there exists a set A of integers such that:
$c_1,c_2$ are absolute constants. In this paper, following these results, we prove that, there exists a set A of integers such that: 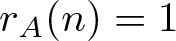 $r_A(n)=1$ for all integers n and
$r_A(n)=1$ for all integers n and 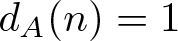 $d_A(n)=1$ for all positive integers n,
$d_A(n)=1$ for all positive integers n, 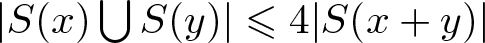 $|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for
$|S(x)\bigcup S(y)|\leqslant 4|S(x+y)|$ for 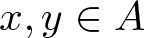 $x,y\in A$ and
$x,y\in A$ and 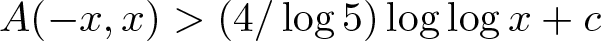 $A(-x,x) \gt (4/\log 5)\log\log x+c$ for all
$A(-x,x) \gt (4/\log 5)\log\log x+c$ for all 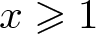 $x\geqslant 1$, where c is an absolute constant. Furthermore, we also construct a family of arbitrarily spare such sets A.
$x\geqslant 1$, where c is an absolute constant. Furthermore, we also construct a family of arbitrarily spare such sets A.