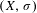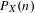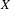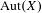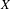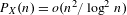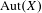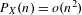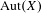Refine search
Actions for selected content:
1 results
The automorphism group of a shift of slow growth is amenable
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 11 December 2018, pp. 1788-1804
- Print publication:
- July 2020
-
- Article
-
- You have access
- Export citation
-
Suppose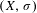
$(X,\unicode[STIX]{x1D70E})$ is a subshift, 
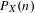$P_{X}(n)$ is the word complexity function of 
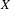$X$, and 
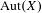$\text{Aut}(X)$ is the group of automorphisms of 
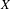$X$. We show that if 
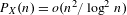$P_{X}(n)=o(n^{2}/\log ^{2}n)$, then 
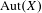$\text{Aut}(X)$ is amenable (as a countable, discrete group). We further show that if 
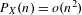$P_{X}(n)=o(n^{2})$, then 
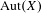$\text{Aut}(X)$ can never contain a non-abelian free monoid (and, in particular, can never contain a non-abelian free subgroup). This is in contrast to recent examples, due to Salo and Schraudner, of subshifts with quadratic complexity that do contain such a monoid.
