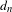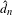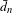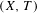1 results
Bounded complexity, mean equicontinuity and discrete spectrum
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 07 October 2019, pp. 494-533
- Print publication:
- February 2021
-
- Article
- Export citation
-
We study dynamical systems that have bounded complexity with respect to three kinds metrics: the Bowen metric
$d_{n}$, the max-mean metric 
$\hat{d}_{n}$ and the mean metric 
$\bar{d}_{n}$, both in topological dynamics and ergodic theory. It is shown that a topological dynamical system 
$(X,T)$ has bounded complexity with respect to 
$d_{n}$ (respectively 
$\hat{d}_{n}$) if and only if it is equicontinuous (respectively equicontinuous in the mean). However, we construct minimal systems that have bounded complexity with respect to 
$\bar{d}_{n}$ but that are not equicontinuous in the mean. It turns out that an invariant measure 
$\unicode[STIX]{x1D707}$ on 
$(X,T)$ has bounded complexity with respect to 
$d_{n}$ if and only if 
$(X,T)$ is 
$\unicode[STIX]{x1D707}$-equicontinuous. Meanwhile, it is shown that 
$\unicode[STIX]{x1D707}$ has bounded complexity with respect to 
$\hat{d}_{n}$ if and only if 
$\unicode[STIX]{x1D707}$ has bounded complexity with respect to 
$\bar{d}_{n}$, if and only if 
$(X,T)$ is 
$\unicode[STIX]{x1D707}$-mean equicontinuous and if and only if it has discrete spectrum.
