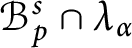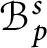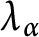In this paper, we give a complete description of closed ideals of the Banach algebra
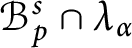 $\mathcal {B}^{s}_{p}\cap \lambda _{\alpha }$
, where
$\mathcal {B}^{s}_{p}\cap \lambda _{\alpha }$
, where
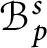 $\mathcal {B}^{s}_{p}$
denotes the analytic Besov space and
$\mathcal {B}^{s}_{p}$
denotes the analytic Besov space and
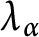 $\lambda _{\alpha }$
is the separable analytic Lipschitz space. Our result extends several previous results in Bahajji-El Idrissi and El-Fallah (2020, Studia Mathematica 255, 209–217), Bouya (2009, Canadian Journal of Mathematics 61, 282–298), and Shirokov (1982, Izv. Ross. Akad. Nauk Ser. Mat. 46, 1316–1332).
$\lambda _{\alpha }$
is the separable analytic Lipschitz space. Our result extends several previous results in Bahajji-El Idrissi and El-Fallah (2020, Studia Mathematica 255, 209–217), Bouya (2009, Canadian Journal of Mathematics 61, 282–298), and Shirokov (1982, Izv. Ross. Akad. Nauk Ser. Mat. 46, 1316–1332).