1 results
On Universal Schauder Bases in Non-Archimedean Fréchet Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 47 / Issue 1 / 01 March 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 108-118
- Print publication:
- 01 March 2004
-
- Article
-
- You have access
- Export citation
-
It is known that any non-archimedean Fréchet space of countable type is isomorphic to a subspace of
$c_{0}^{\mathbb{N}}$. In this paper we prove that there exists a non-archimedean Fréchet space 
$U$ with a basis 
$({{u}_{n}})$ such that any basis 
$({{x}_{n}})$ in a non-archimedean Fréchet space 
$X$ is equivalent to a subbasis 
$({{u}_{kn}})$ of $({{u}_{n}})$. Then any non-archimedean Fréchet space with a basis is isomorphic to a complemented subspace of $U$. In contrast to this, we show that a non-archimedean Fréchet space $X$ with a basis $({{x}_{n}})$ is isomorphic to a complemented subspace of $c_{0}^{\mathbb{N}}$ if and only if $X$ is isomorphic to one of the following spaces: 
${{c}_{0}},\,{{c}_{0}}\,\times \,{{\mathbb{K}}^{\mathbb{N}}},\,{{\mathbb{K}}^{\mathbb{N}}},\,c_{0}^{\mathbb{N}}$. Finally, we prove that there is no nuclear non-archimedean Fréchet space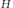 
$H$ with a basis 
$({{h}_{n}})$ such that any basis 
$({{y}_{n}})$ in a nuclear non-archimedean Fréchet space 
$Y$ is equivalent to a subbasis 
$({{h}_{kn}})$ of $({{h}_{n}})$.
