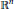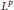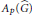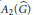Refine search
Actions for selected content:
6 results
Quasilinear duality and inversion in Banach spaces
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 11 January 2024, pp. 1223-1239
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE STABILITY OF THE DIFFERENTIAL PROCESS GENERATED BY COMPLEX INTERPOLATION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 20 August 2020, pp. 303-334
- Print publication:
- January 2022
-
- Article
- Export citation
23 - Haagerup’s characterizations of the WEP
-
- Book:
- Tensor Products of <I>C</I>*-Algebras and Operator Spaces
- Published online:
- 10 February 2020
- Print publication:
- 27 February 2020, pp 384-409
-
- Chapter
- Export citation
Interpolation of Morrey Spaces on Metric Measure Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 3 / 01 September 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 598-608
- Print publication:
- 01 September 2014
-
- Article
-
- You have access
- Export citation
Representing Multipliers of the Fourier Algebra on Non-Commutative Lp Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 63 / Issue 4 / 01 August 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 798-825
- Print publication:
- 01 August 2011
-
- Article
-
- You have access
- Export citation
Generalized Amalgams, With Applications to Fourier Transform
-
- Journal:
- Canadian Journal of Mathematics / Volume 42 / Issue 3 / 01 June 1990
- Published online by Cambridge University Press:
- 20 November 2018, pp. 395-409
- Print publication:
- 01 June 1990
-
- Article
-
- You have access
- Export citation