We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
A generically embedded real submanifold of codimension two in a complex manifold has isolated complex points that can be classified as either elliptic or hyperbolic. In this paper we show that a pair consisting of one elliptic and one hyperbolic complex point of the same sign can be cancelled by a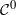 
$\mathcal {C}^{0}$small isotopy of embeddings.
