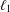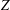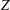Refine search
Actions for selected content:
15 results
4 - Optimization: Hard Computing
-
- Book:
- Introduction to Intelligent Systems, Control, and Machine Learning using MATLAB
- Published online:
- 27 November 2023
- Print publication:
- 16 November 2023, pp 109-141
-
- Chapter
- Export citation
Appendix - Other Numerical Methods
-
- Book:
- Density Matrix and Tensor Network Renormalization
- Published online:
- 18 January 2024
- Print publication:
- 31 August 2023, pp 394-407
-
- Chapter
- Export citation
7 - Non-linear Optimization
-
- Book:
- Introduction to Environmental Data Science
- Published online:
- 23 March 2023
- Print publication:
- 23 March 2023, pp 216-244
-
- Chapter
- Export citation
6 - Numerical Minimization Process
- from Part II - Practical Tools
-
- Book:
- Principles of Data Assimilation
- Published online:
- 22 September 2022
- Print publication:
- 29 September 2022, pp 128-160
-
- Chapter
- Export citation
MATRIX ANALYSES ON THE DAI–LIAO CONJUGATE GRADIENT METHOD
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 09 May 2019, pp. 195-203
-
- Article
-
- You have access
- Export citation
A NEW DERIVATIVE-FREE CONJUGATE GRADIENT METHOD FOR LARGE-SCALE NONLINEAR SYSTEMS OF EQUATIONS
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 22 March 2017, pp. 500-511
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
A MODIFIED FR CONJUGATE GRADIENT METHOD FOR COMPUTING
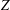 $Z$ -EIGENPAIRS OF SYMMETRIC TENSORS
$Z$ -EIGENPAIRS OF SYMMETRIC TENSORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 26 July 2016, pp. 411-420
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
Conjugate Gradient Method for Estimation of Robin Coefficients
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 4 / Issue 2 / May 2014
- Published online by Cambridge University Press:
- 28 May 2015, pp. 189-204
- Print publication:
- May 2014
-
- Article
- Export citation
Spectral Optimization Methods for the Time Fractional Diffusion Inverse Problem
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 6 / Issue 3 / August 2013
- Published online by Cambridge University Press:
- 28 May 2015, pp. 499-519
- Print publication:
- August 2013
-
- Article
- Export citation
A least-squares method for the numerical solution of theDirichlet problem for the elliptic monge − ampère equation in dimension two∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 19 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 03 June 2013, pp. 780-810
- Print publication:
- July 2013
-
- Article
- Export citation
ITERATIVE SOLUTION OF SHIFTED POSITIVE-DEFINITE LINEAR SYSTEMS ARISING IN A NUMERICAL METHOD FOR THE HEAT EQUATION BASED ON LAPLACE TRANSFORMATION AND QUADRATURE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 53 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 15 August 2012, pp. 134-155
-
- Article
-
- You have access
- Export citation
Preconditioners and Electron Density Optimization in Orbital-Free Density Functional Theory
-
- Journal:
- Communications in Computational Physics / Volume 12 / Issue 1 / July 2012
- Published online by Cambridge University Press:
- 20 August 2015, pp. 135-161
- Print publication:
- July 2012
-
- Article
- Export citation
Algebraic Multigrid Preconditioning for Finite Element Solution of Inhomogeneous Elastic Inclusion Problems in Articular Cartilage
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 3 / Issue 6 / December 2011
- Published online by Cambridge University Press:
- 03 June 2015, pp. 729-744
- Print publication:
- December 2011
-
- Article
- Export citation
Construction of Probabilistic Boolean Networks from a Prescribed Transition Probability Matrix: A Maximum Entropy Rate Approach
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 1 / Issue 2 / May 2011
- Published online by Cambridge University Press:
- 28 May 2015, pp. 132-154
- Print publication:
- May 2011
-
- Article
- Export citation