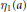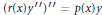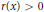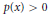3 results
Geodesic Flows Modelled by Expansive Flows
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 August 2018, pp. 61-95
-
- Article
- Export citation
Comparison Theorem for Conjugate Points of a Fourth-order Linear Differential Equation
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 1 / 01 March 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 39-43
- Print publication:
- 01 March 2013
-
- Article
-
- You have access
- Export citation
-
In 1961, J. Barrett showed that if the first conjugate point
${{\eta }_{1}}\left( a \right)$ exists for the differential equation 
${{\left( r\left( x \right){y}'' \right)}^{\prime \prime }}=p\left( x \right)y$, where 
$r\left( x \right)\,>\,0$ and 
$p\left( x \right)\,>\,0$, then so does the first systems-conjugate point 
${{\hat{\eta }}_{1}}\left( a \right)$. The aim of this note is to extend this result to the general equation with middle term 
${{\left( q\left( x \right){y}' \right)}^{\prime }}$ without further restriction on 
$q\left( x \right)$, other than continuity.
Regularity and variationality of solutionsto Hamilton-Jacobi equations. Part I: Regularity (errata)
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 13 / Issue 2 / April 2007
- Published online by Cambridge University Press:
- 12 May 2007, pp. 413-417
- Print publication:
- April 2007
-
- Article
- Export citation
