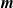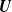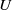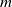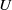We study (asymmetric) 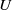 $U$-statistics based on a stationary sequence of
$U$-statistics based on a stationary sequence of 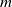 $m$-dependent variables; moreover, we consider constrained
$m$-dependent variables; moreover, we consider constrained 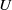 $U$-statistics, where the defining multiple sum only includes terms satisfying some restrictions on the gaps between indices. Results include a law of large numbers and a central limit theorem, together with results on rate of convergence, moment convergence, functional convergence, and a renewal theory version.
$U$-statistics, where the defining multiple sum only includes terms satisfying some restrictions on the gaps between indices. Results include a law of large numbers and a central limit theorem, together with results on rate of convergence, moment convergence, functional convergence, and a renewal theory version.
Special attention is paid to degenerate cases where, after the standard normalization, the asymptotic variance vanishes; in these cases non-normal limits occur after a different normalization.
The results are motivated by applications to pattern matching in random strings and permutations. We obtain both new results and new proofs of old results.
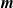 $\boldsymbol{m}$-dependent and constrained
$\boldsymbol{m}$-dependent and constrained 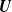 $\boldsymbol{U}$-statistics, with applications to pattern matching in random strings and permutations
$\boldsymbol{U}$-statistics, with applications to pattern matching in random strings and permutations