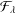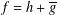2 results
14 - Vectors, Preferences and Convexity
-
- Book:
- Mathematics for Economics and Finance
- Published online:
- 24 May 2024
- Print publication:
- 30 May 2024, pp 137-151
-
- Chapter
- Export citation
ON CONVEX COMBINATIONS OF CONVEX HARMONIC MAPPINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 07 August 2017, pp. 256-262
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation