Two sets 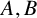 $A,B$ of positive integers are called exact additive complements if
$A,B$ of positive integers are called exact additive complements if 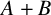 $A+B$ contains all sufficiently large integers and
$A+B$ contains all sufficiently large integers and 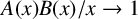 $A(x)B(x)/x\rightarrow 1$. For
$A(x)B(x)/x\rightarrow 1$. For 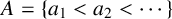 $A=\{a_1<a_2<\cdots \}$, let
$A=\{a_1<a_2<\cdots \}$, let 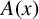 $A(x)$ denote the counting function of A and let
$A(x)$ denote the counting function of A and let 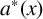 $a^*(x)$ denote the largest element in
$a^*(x)$ denote the largest element in 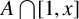 $A\bigcap [1,x]$. Following the work of Ruzsa [‘Exact additive complements’, Quart. J. Math. 68 (2017) 227–235] and Chen and Fang [‘Additive complements with Narkiewicz’s condition’, Combinatorica 39 (2019), 813–823], we prove that, for exact additive complements
$A\bigcap [1,x]$. Following the work of Ruzsa [‘Exact additive complements’, Quart. J. Math. 68 (2017) 227–235] and Chen and Fang [‘Additive complements with Narkiewicz’s condition’, Combinatorica 39 (2019), 813–823], we prove that, for exact additive complements 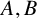 $A,B$ with
$A,B$ with 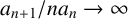 ${a_{n+1}}/ {na_n}\rightarrow \infty $,
${a_{n+1}}/ {na_n}\rightarrow \infty $, 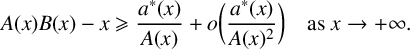 $$ \begin{align*}A(x)B(x)-x\geqslant \frac{a^*(x)}{A(x)}+o\bigg(\frac{a^*(x)}{A(x)^2}\bigg) \quad\mbox{as } x\rightarrow +\infty.\end{align*} $$
$$ \begin{align*}A(x)B(x)-x\geqslant \frac{a^*(x)}{A(x)}+o\bigg(\frac{a^*(x)}{A(x)^2}\bigg) \quad\mbox{as } x\rightarrow +\infty.\end{align*} $$
We also construct exact additive complements 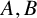 $A,B$ with
$A,B$ with 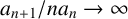 ${a_{n+1}}/{na_n}\rightarrow \infty $ such that
${a_{n+1}}/{na_n}\rightarrow \infty $ such that 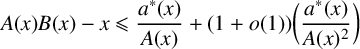 $$ \begin{align*}A(x)B(x)-x\leqslant \frac{a^*(x)}{A(x)}+(1+o(1))\bigg(\frac{a^*(x)}{A(x)^2}\bigg)\end{align*} $$
$$ \begin{align*}A(x)B(x)-x\leqslant \frac{a^*(x)}{A(x)}+(1+o(1))\bigg(\frac{a^*(x)}{A(x)^2}\bigg)\end{align*} $$
for infinitely many positive integers x.
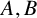
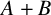
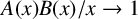
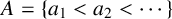
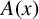
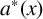
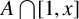
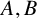
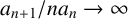
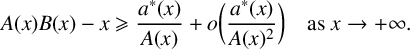
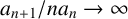
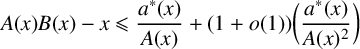

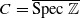 over 𝔽
over 𝔽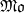 -schemes to interpret conceptually the spectral realization of zeros of
-schemes to interpret conceptually the spectral realization of zeros of 