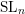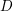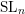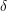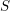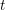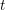Refine search
Actions for selected content:
4 results
A support theorem for Hilbert schemes of planar curves, II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 28 April 2021, pp. 835-882
- Print publication:
- April 2021
-
- Article
- Export citation
A support theorem for the Hitchin fibration: the case of
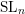 $\text{SL}_{n}$
$\text{SL}_{n}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 6 / June 2017
- Published online by Cambridge University Press:
- 26 April 2017, pp. 1316-1347
- Print publication:
- June 2017
-
- Article
- Export citation
Mixed motivic sheaves (and weights for them) exist if ‘ordinary’ mixed motives do
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 5 / May 2015
- Published online by Cambridge University Press:
- 09 January 2015, pp. 917-956
- Print publication:
- May 2015
-
- Article
- Export citation
Purity and decomposition theorems for staggered sheaves
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 02 April 2012, pp. 695-745
- Print publication:
- October 2012
-
- Article
- Export citation