1 results
Γ-convergence and stochastic homogenization of degenerate integral functionals in weighted Sobolev spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 08 February 2022, pp. 491-544
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
We study the $\Gamma$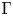
-convergence of nonconvex vectorial integral functionals whose integrands satisfy possibly degenerate growth and coercivity conditions. The latter involve suitable scale-dependent weight functions. We prove that under appropriate uniform integrability conditions on the weight functions, which shall belong to a Muckenhoupt class, the corresponding functionals $\Gamma$
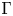-converge, up to subsequences, to a degenerate integral functional defined on a limit weighted Sobolev space. The general analysis is then applied to the case of random stationary integrands and weights to prove a stochastic homogenization result for the corresponding functionals.
