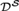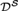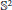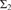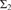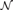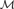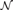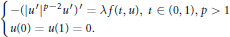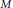10 results
A class of Hessian quotient equations in de Sitter space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 805-821
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
Periodic solutions for one-dimensional nonlinear nonlocal problem with drift including singular nonlinearities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 23 December 2021, pp. 229-261
- Print publication:
- February 2023
-
- Article
- Export citation
Periodic solutions for a second-order differential equation with indefinite weak singularity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 15 January 2019, pp. 1135-1152
- Print publication:
- October 2019
-
- Article
- Export citation
Periodic solutions for indefinite singular perturbations of the relativistic acceleration
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 22 June 2018, pp. 703-712
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
WEAKLY 2-RANDOMS AND 1-GENERICS IN SCOTT SETS
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 01 May 2018, pp. 392-394
- Print publication:
- March 2018
-
- Article
- Export citation
Periodic Solutions of an Indefinite Singular Equation Arising from the Kepler Problem on the Sphere
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 1 / 01 February 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 173-190
- Print publication:
- 01 February 2018
-
- Article
-
- You have access
- Export citation
ON THE DECIDABILITY OF THE
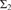 ${{\rm{\Sigma }}_2}$ THEORIES OF THE ARITHMETIC AND HYPERARITHMETIC DEGREES AS UPPERSEMILATTICES
${{\rm{\Sigma }}_2}$ THEORIES OF THE ARITHMETIC AND HYPERARITHMETIC DEGREES AS UPPERSEMILATTICES
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 09 January 2018, pp. 1496-1518
- Print publication:
- December 2017
-
- Article
- Export citation
An Ambrosetti–Prodi-type result for a quasilinear Neumann problem
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 3 / October 2012
- Published online by Cambridge University Press:
- 26 July 2012, pp. 771-780
-
- Article
-
- You have access
- Export citation
Existence and Multiplicity of Positive Solutions for Singular Semipositone p-Laplacian Equations
-
- Journal:
- Canadian Journal of Mathematics / Volume 58 / Issue 3 / 01 June 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 449-475
- Print publication:
- 01 June 2006
-
- Article
-
- You have access
- Export citation
On positive solutions of some semilinear elliptic equations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 3 / June 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 343-355
- Print publication:
- June 1991
-
- Article
-
- You have access
- Export citation