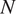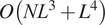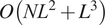15 results
1 - Introduction and Overview
-
- Book:
- Signals, Systems, and Signal Processing
- Published online:
- 29 August 2024
- Print publication:
- 13 June 2024, pp 1-9
-
- Chapter
- Export citation
Fast principal component analysis for cryo-electron microscopy images
-
- Journal:
- Biological Imaging / Volume 3 / 2023
- Published online by Cambridge University Press:
- 03 February 2023, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Improving Quantitative EDS Chemical Analysis of Alloy Nanoparticles by PCA Denoising: Part II. Uncertainty Intervals
-
- Journal:
- / Volume 28 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 18 April 2022, pp. 723-731
- Print publication:
- June 2022
-
- Article
- Export citation
Improving Quantitative EDS Chemical Analysis of Alloy Nanoparticles by PCA Denoising: Part I, Reducing Reconstruction Bias
-
- Journal:
- / Volume 28 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 03 January 2022, pp. 338-349
- Print publication:
- April 2022
-
- Article
- Export citation
Estimation of intrapulse modulation parameters of LPI radar under noisy conditions
-
- Journal:
- International Journal of Microwave and Wireless Technologies / Volume 14 / Issue 9 / November 2022
- Published online by Cambridge University Press:
- 03 December 2021, pp. 1177-1194
-
- Article
- Export citation
Developing and Evaluating Deep Neural Network-Based Denoising for Nanoparticle TEM Images with Ultra-Low Signal-to-Noise
-
- Journal:
- / Volume 27 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 1431-1447
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ultra-Fast Electron Microscopic Imaging of Single Molecules With a Direct Electron Detection Camera and Noise Reduction
-
- Journal:
- / Volume 26 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 20 July 2020, pp. 667-675
- Print publication:
- August 2020
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Frequency Domain Design Method of Wavelet Basis Based on Pulsar Signal
-
- Journal:
- The Journal of Navigation / Volume 73 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 16 June 2020, pp. 1223-1236
- Print publication:
- November 2020
-
- Article
- Export citation
Noise bias compensation for tone mapped noisy image using prior knowledge
-
- Journal:
- APSIPA Transactions on Signal and Information Processing / Volume 8 / 2019
- Published online by Cambridge University Press:
- 04 January 2019, e3
- Print publication:
- 2019
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Image Denoising via Residual Kurtosis Minimization
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 8 / Issue 3 / August 2015
- Published online by Cambridge University Press:
- 05 August 2015, pp. 406-424
- Print publication:
- August 2015
-
- Article
- Export citation
A COMBINED FIRST-ORDER AND SECOND-ORDER VARIATION APPROACH FOR MULTIPLICATIVE NOISE REMOVAL
-
- Journal:
- The ANZIAM Journal / Volume 56 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 22 December 2014, pp. 116-137
-
- Article
-
- You have access
- Export citation
Photobleaching/Photoblinking Differential Equation Model for Fluorescence Microscopy Imaging
-
- Journal:
- / Volume 19 / Issue 5 / October 2013
- Published online by Cambridge University Press:
- 02 September 2013, pp. 1110-1121
- Print publication:
- October 2013
-
- Article
- Export citation
Augmented Lagrangian Methods for p-Harmonic Flows with the Generalized Penalization Terms and Application to Image Processing
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 6 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 28 May 2015, pp. 1-20
- Print publication:
- February 2013
-
- Article
- Export citation
3D Data Denoising Using Combined SparseDictionaries
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 1 / 2013
- Published online by Cambridge University Press:
- 28 January 2013, pp. 60-74
- Print publication:
- 2013
-
- Article
- Export citation
SURE shrinkage of Gaussian paths and signal identification*
-
- Journal:
- ESAIM: Probability and Statistics / Volume 15 / 2011
- Published online by Cambridge University Press:
- 05 January 2012, pp. 180-196
- Print publication:
- 2011
-
- Article
- Export citation