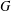5 results
THE
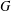 $G$-CENTRE AND GRADABLE DERIVED EQUIVALENCES
$G$-CENTRE AND GRADABLE DERIVED EQUIVALENCES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 18 June 2018, pp. 289-315
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Cremona transformations and derived equivalences of K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 7 / July 2018
- Published online by Cambridge University Press:
- 28 May 2018, pp. 1508-1533
- Print publication:
- July 2018
-
- Article
-
- You have access
- HTML
- Export citation
Window shifts, flop equivalences and Grassmannian twists
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 6 / June 2014
- Published online by Cambridge University Press:
- 07 April 2014, pp. 942-978
- Print publication:
- June 2014
-
- Article
- Export citation
Equivalences and stratified flops
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 09 November 2011, pp. 185-208
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
Picard Groups for Derived Module Categories
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 87 / Issue 1 / July 2003
- Published online by Cambridge University Press:
- 25 June 2003, pp. 197-225
- Print publication:
- July 2003
-
- Article
- Export citation