1 results
PARTITIONS WITH AN ARBITRARY NUMBER OF SPECIFIED DISTANCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 03 June 2019, pp. 35-39
- Print publication:
- February 2020
-
- Article
- Export citation
-
For positive integers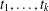
$t_{1},\ldots ,t_{k}$, let 
$\tilde{p}(n,t_{1},t_{2},\ldots ,t_{k})$ (respectively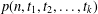 
$p(n,t_{1},t_{2},\ldots ,t_{k})$) be the number of partitions of 
$n$ such that, if 
$m$ is the smallest part, then each of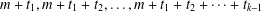 
$m+t_{1},m+t_{1}+t_{2},\ldots ,m+t_{1}+t_{2}+\cdots +t_{k-1}$ appears as a part and the largest part is at most (respectively equal to) 
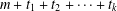$m+t_{1}+t_{2}+\cdots +t_{k}$. Andrews et al. [‘Partitions with fixed differences between largest and smallest parts’, Proc. Amer. Math. Soc.143 (2015), 4283–4289] found an explicit formula for the generating function of 
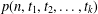$p(n,t_{1},t_{2},\ldots ,t_{k})$. We establish a 
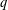$q$-series identity from which the formulae for the generating functions of 
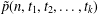$\tilde{p}(n,t_{1},t_{2},\ldots ,t_{k})$ and 
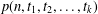$p(n,t_{1},t_{2},\ldots ,t_{k})$ can be obtained.
