A first-order theory is equational if every definable set is a Boolean combination of instances of equations, that is, of formulae such that the family of finite intersections of instances has the descending chain condition. Equationality is a strengthening of stability. We show the equationality of the theory of proper extensions of algebraically closed fields and of the theory of separably closed fields of arbitrary imperfection degree.

Analysability of finite U-rank types are explored both in general and in the theory ${\rm{DC}}{{\rm{F}}_0}$. The well-known fact that the equation $\delta \left( {{\rm{log}}\,\delta x} \right) = 0$ is analysable in but not almost internal to the constants is generalized to show that $\underbrace {{\rm{log}}\,\delta \cdots {\rm{log}}\,\delta }_nx = 0$ is not analysable in the constants in $\left( {n - 1} \right)$-steps. The notion of a canonical analysis is introduced–-namely an analysis that is of minimal length and interalgebraic with every other analysis of that length. Not every analysable type admits a canonical analysis. Using properties of reductions and coreductions in theories with the canonical base property, it is constructed, for any sequence of positive integers $\left( {{n_1}, \ldots ,{n_\ell }} \right)$, a type in ${\rm{DC}}{{\rm{F}}_0}$ that admits a canonical analysis with the property that the ith step has U-rank ${n_i}$.

The degree spectrum of a countable structure is the set of all Turing degrees of presentations of that structure. We show that every nonlow Turing degree lies in the spectrum of some differentially closed field (of characteristic 0, with a single derivation) whose spectrum does not contain the computable degree 0. Indeed, this is an equivalence, for we also show that if this spectrum contained a low degree, then it would contain the degree 0. From these results we conclude that the spectra of differentially closed fields of characteristic 0 are exactly the jump-preimages of spectra of automorphically nontrivial graphs.

Suppose p is the generic type of a differential-algebraic jet space to a finite dimensional differential-algebraic variety at a generic point. It is shown that p satisfies a certain strengthening of almost internality to the constants. This strengthening, which was originally called “being Moishezon to the constants” in [9] but is here renamed preserving internality to the constants, is a model-theoretic abstraction of the generic behaviour of jet spaces in complex-analytic geometry. An example is given showing that only a generic analogue holds in the differential-algebraic case: there is a finite dimensional differential-algebraic variety X with a subvariety Z that is internal to the constants, such that the restriction of the differential-algebraic tangent bundle of X to Z is not almost internal to the constants.

We prove that if 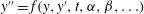$y''=f(y,y',t,\alpha ,\beta ,\ldots)$ is a generic Painlevé equation from among the classes II, IV and V, and if 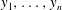$y_1,\ldots,y_n$ are distinct solutions, then 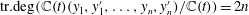$\mathrm{tr.deg}(\mathbb{C}(t)(y_1,y'_1,\ldots,y_n,y'_n)/\mathbb{C}(t))=2n$. (This was proved by Nishioka for the single equation 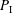$P_{{\rm I}}$.) For generic Painlevé III and VI, we have a slightly weaker result: 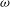$\omega $-categoricity (in the sense of model theory) of the solution space, as described below. The results confirm old beliefs about the Painlevé transcendents.

We apply the collapse techniques to Poizat's red differential field in order to obtain differentially closed fields of Morley rank ω·2 each equipped with an additive definable subgroup of rank ω. By means of the logarithmic derivative, we obtain a green field of rank ω·2 with a multiplicative definable divisible subgroup containing the field of constants, which is again definable in the reduct of the green field.