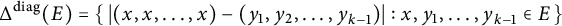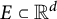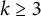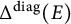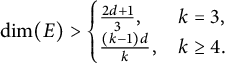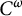Search

We introduce a class of Falconer distance problems, which we call of restricted type, lying between the classical version and its pinned variant. Prototypical restricted distance sets are the diagonal distance sets, k-point configuration sets given by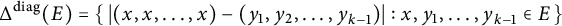

$$ \begin{align*}\Delta^{\mathrm{diag}}(E)= \{ \,|(x,x,\dots,x)-(y_1,y_2,\dots,y_{k-1})| : x, y_1, \dots,y_{k-1} \in E\, \}\end{align*} $$

for a compact

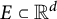$E\subset \mathbb {R}^d$ and

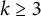$k\ge 3$. We show that

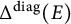$\Delta ^{\mathrm{diag}}(E)$ has non-empty interior if the Hausdorff dimension of E satisfies (0.1)

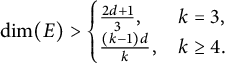$$ \begin{align} \dim(E)> \begin{cases} \frac{2d+1}3, & k=3, \\ \frac{(k-1)d}k,& k\ge 4. \end{cases} \end{align} $$

We prove an extension of this to

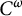$C^\omega $ Riemannian metrics g close to the product of Euclidean metrics. For product metrics, this follows from known results on pinned distance sets, but to obtain a result for general perturbations g, we present a sequence of proofs of partial results, leading up to the proof of the full result, which is based on estimates for multilinear Fourier integral operators.

We show that products of sufficiently thick Cantor sets generate trees in the plane with constant distance between adjacent vertices. Moreover, we prove that the set of choices for this distance has non-empty interior. We allow our trees to be countably infinite, which further distinguishes this work from previous results on patterns in fractal sets. This builds on the authors’ previous work on graphs and distance sets over products of Cantor sets of sufficient Newhouse thickness.

Search Results

Refine search

Refine search

Actions for selected content:

2 results

On restricted Falconer distance sets

Infinite constant gap length trees in products of thick Cantor sets

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

2 results

On restricted Falconer distance sets

Infinite constant gap length trees in products of thick Cantor sets