2 results
DOUBLING TROPICAL
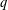 $q$-DIFFERENCE ANALOGUE OF THE LEMMA ON THE LOGARITHMIC
DERIVATIVE
$q$-DIFFERENCE ANALOGUE OF THE LEMMA ON THE LOGARITHMIC
DERIVATIVE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 12 September 2018, pp. 474-480
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
HILBERT TRANSFORMS ALONG CURVES IN THE HEISENBERG GROUP
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 80 / Issue 3 / May 2000
- Published online by Cambridge University Press:
- 20 August 2001, pp. 611-642
- Print publication:
- May 2000
-
- Article
- Export citation