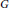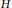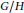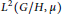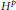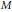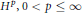7 results
16 - Convex Optimization
- from Part III - Nonlinear Equations and Optimization
-
- Book:
- Classical Numerical Analysis
- Published online:
- 29 September 2022
- Print publication:
- 20 October 2022, pp 451-506
-
- Chapter
- Export citation
6 - Linear Operators
- from Part II - Elements Of Classical Functional Analysis
-
- Book:
- Classical and Discrete Functional Analysis with Measure Theory
- Published online:
- 06 January 2022
- Print publication:
- 20 January 2022, pp 214-252
-
- Chapter
- Export citation
11 - Banach Space Basics
- from Part III - The Banach Space Setting
-
- Book:
- Operator-Adapted Wavelets, Fast Solvers, and Numerical Homogenization
- Published online:
- 10 October 2019
- Print publication:
- 24 October 2019, pp 151-153
-
- Chapter
- Export citation
Abstract Plancherel (Trace) Formulas over Homogeneous Spaces of Compact Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 1 / 01 March 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 111-121
- Print publication:
- 01 March 2017
-
- Article
-
- You have access
- Export citation
A quasi-dual Lagrange multiplier space for serendipity mortar finite elements in 3D
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 1 / January 2004
- Published online by Cambridge University Press:
- 15 February 2004, pp. 73-92
- Print publication:
- January 2004
-
- Article
- Export citation
A Comparison of Dual Lagrange Multiplier Spaces for Mortar Finite Element Discretizations
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 6 / November 2002
- Published online by Cambridge University Press:
- 15 January 2003, pp. 995-1012
- Print publication:
- November 2002
-
- Article
- Export citation
On the Smirnov Class Defined by the Maximal Function
-
- Journal:
- Canadian Mathematical Bulletin / Volume 45 / Issue 2 / 01 June 2002
- Published online by Cambridge University Press:
- 20 November 2018, pp. 265-271
- Print publication:
- 01 June 2002
-
- Article
-
- You have access
- Export citation