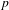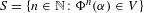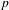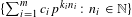Refine search
Actions for selected content:
1 results
THE DYNAMICAL MORDELL–LANG CONJECTURE FOR ENDOMORPHISMS OF SEMIABELIAN VARIETIES DEFINED OVER FIELDS OF POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 24 June 2019, pp. 669-698
- Print publication:
- March 2021
-
- Article
- Export citation