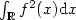1 results
Adaptive estimation of a quadratic functional of a density by model selection
-
- Journal:
- ESAIM: Probability and Statistics / Volume 9 / February 2005
- Published online by Cambridge University Press:
- 15 November 2005, pp. 1-18
- Print publication:
- February 2005
-
- Article
- Export citation