1 results
Positive solutions to the prey–predator equations with dormancy of predators
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 24 April 2023, pp. 96-108
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
The time-global unique classical positive solutions to the reaction–diffusion equations for prey–predator models with dormancy of predators are constructed. The feature appears on the nonlinear terms of Holling type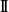
$\rm I\!I$ functional response. The crucial step is to establish time-local positive classical solutions by using a new approximation associated with time-evolution operators. Although the system does not equip usual comparison principle for solutions to partial differential equation, a priori bounds are derived by enclosing and renormalising arguments of solutions to the corresponding ordinary differential equations. Furthermore, time-global existence, invariant regions and asymptotic behaviours of solutions follow from such a priori bounds.
