1 results
On the Dispersive Estimate for the Dirichlet Schrödinger Propagator and Applications to Energy Critical NLS
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 5 / 01 October 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1110-1142
- Print publication:
- 01 October 2014
-
- Article
-
- You have access
- Export citation
-
We consider the obstacle problem for the Schrödinger evolution in the exterior of the unit ball with Dirichlet boundary condition. Under radial symmetry we compute explicitly the fundamental solution for the linear Dirichlet Schrödinger propagator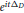
${{e}^{it{{\Delta }_{D}}}}$ and give a robust algorithm to prove sharp 
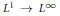${{L}^{1}}\,\to \,{{L}^{\infty }}$ dispersive estimates. We showcase the analysis in dimensions 
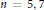$n\,=\,5,\,7$. As an application, we obtain global well-posedness and scattering for defocusing energy-critical 
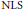$\text{NLS}$ on 
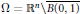$\Omega \,=\,{{\mathbb{R}}^{n}}\backslash \overline{B\left( 0,\,1 \right)}$ with Dirichlet boundary condition and radial data in these dimensions.
