We consider the ergodic (or additive eigenvalue) problem for the Neumann-type boundary-value problem for Hamilton–Jacobi equations and the corresponding discounted problems. Denoting by uλ the solution of the discounted problem with discount factor λ > 0, we establish the convergence of the whole family 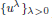to a solution of the ergodic problem as λ → 0, and give a representation formula for the limit function via the Mather measures and Peierls function. As an interesting by-product, we introduce Mather measures associated with Hamilton–Jacobi equations with the Neumann-type boundary conditions. These results are variants of the main results in a recent paper by Davini et al., who study the same convergence problem on smooth compact manifolds without boundary.

This paper concerns continuous dependence estimates for Hamilton-Jacobi-Bellman-Isaacsoperators. We establish such an estimate for the parabolic Cauchy problem in the wholespace  [0, +∞) × ℝn and, under some periodicity and eitherellipticity or controllability assumptions, we deduce a similar estimate for the ergodicconstant associated to the operator. An interesting byproduct of the latter result will bethe local uniform convergence for some classes of singular perturbation problems.