1 results
Local escape rates for
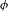$\unicode[STIX]{x1D719}$-mixing dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 10 / October 2020
- Published online by Cambridge University Press:
- 25 July 2019, pp. 2854-2880
- Print publication:
- October 2020
-
- Article
- Export citation
-
We show that dynamical systems with
$\unicode[STIX]{x1D719}$-mixing measures have local escape rates which are exponential with rate 1 at non-periodic points and equal to the extremal index at periodic points. We apply this result to equilibrium states on subshifts of finite type, Gibbs–Markov systems, expanding interval maps, Gibbs states on conformal repellers, and more generally to Young towers, and by extension to all systems that can be modeled by a Young tower.
