Refine search
Actions for selected content:
5 results
Optimal control of the bidomain system (III): Existence ofminimizers and first-order optimality conditions
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 47 / Issue 4 / July 2013
- Published online by Cambridge University Press:
- 13 June 2013, pp. 1077-1106
- Print publication:
- July 2013
-
- Article
- Export citation
Semicontinuity theorem in the micropolar elasticity
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 16 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 10 February 2009, pp. 337-355
- Print publication:
- April 2010
-
- Article
- Export citation
THE SET OF SOLUTIONS OF INTEGRODIFFERENTIAL EQUATIONS IN BANACH SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 507-522
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Existence theorem for nonlinear micropolar elasticity
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 16 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 21 October 2008, pp. 92-110
- Print publication:
- January 2010
-
- Article
- Export citation
A Note on Class Field Theory for Two-Dimensional Local Rings
-
- Journal:
- Compositio Mathematica / Volume 124 / Issue 3 / December 2000
- Published online by Cambridge University Press:
- 04 December 2007, pp. 305-340
- Print publication:
- December 2000
-
- Article
-
- You have access
- Export citation
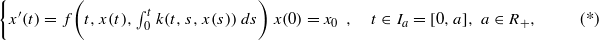
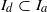 .
.