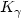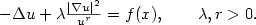Research Article
Unique continuation principle for systemsof parabolic equations
-
- Published online by Cambridge University Press:
- 10 February 2009, pp. 247-274
-
- Article
- Export citation
Projective Reeds-Shepp car on S 2 with quadratic cost
-
- Published online by Cambridge University Press:
- 19 December 2008, pp. 275-297
-
- Article
- Export citation
Observability properties of a semi-discrete 1d wave equation derived from a mixed finite element methodon nonuniform meshes
-
- Published online by Cambridge University Press:
- 19 December 2008, pp. 298-326
-
- Article
- Export citation
Uniqueness of solutions for some elliptic equations with a quadratic gradient term
-
- Published online by Cambridge University Press:
- 19 December 2008, pp. 327-336
-
- Article
- Export citation
Semicontinuity theorem in the micropolar elasticity
-
- Published online by Cambridge University Press:
- 10 February 2009, pp. 337-355
-
- Article
- Export citation
Global controllability and stabilization for the nonlinear Schrödinger equation on an interval
-
- Published online by Cambridge University Press:
- 10 February 2009, pp. 356-379
-
- Article
- Export citation
Maxwell strata in sub-Riemannian problemon the group of motions of a plane
-
- Published online by Cambridge University Press:
- 21 April 2009, pp. 380-399
-
- Article
- Export citation
Optimal control of the Primitive Equations of the ocean with Lagrangian observations
-
- Published online by Cambridge University Press:
- 21 April 2009, pp. 400-419
-
- Article
- Export citation
Stabilization of second order evolution equationswith unbounded feedback with delay
-
- Published online by Cambridge University Press:
- 21 April 2009, pp. 420-456
-
- Article
- Export citation
Necessary conditions for weak lower semicontinuityon domains with infinite measure
-
- Published online by Cambridge University Press:
- 21 April 2009, pp. 457-471
-
- Article
- Export citation
Oscillations and concentrations generatedby
 -freemappings and weak lower semicontinuityof integral functionals
-freemappings and weak lower semicontinuityof integral functionals
-
- Published online by Cambridge University Press:
- 21 April 2009, pp. 472-502
-
- Article
- Export citation