Refine search
Actions for selected content:
1 results
Fast Evaluation of the Caputo Fractional Derivative and its Applications to Fractional Diffusion Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 07 February 2017, pp. 650-678
- Print publication:
- March 2017
-
- Article
- Export citation
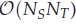 memory and
memory and  work, where
work, where 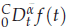 of order
of order 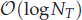 for
for 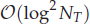 for
for 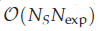 storage and
storage and 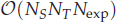 work when numerically solving the time fractional PDEs. Furthermore, we also give the stability and error analysis of the new scheme, and present several numerical examples to demonstrate the performance of our scheme.
work when numerically solving the time fractional PDEs. Furthermore, we also give the stability and error analysis of the new scheme, and present several numerical examples to demonstrate the performance of our scheme.