Let $G$ be a simply-connected, semisimple algebraic group
over $k$, an algebraically closed field of characteristic
zero. Let ${\cal O}_{\epsilon}[G]$ be the quantized function
algebra of $G$ at a primitive $\ell$th root of unity
$\epsilon$, and let $\overline{{\cal O}_{\epsilon}[G]}$ be the
`restricted' quantized function algebra at $\epsilon$,
a finite-dimensional $k$-algebra obtained from
${\cal O}_{\epsilon}[G]$ by factoring out a centrally generated
ideal. It is known that $\overline{{\cal O}_{\epsilon}[G]}$ is
a Hopf algebra. We study the cohomology ring
$\mbox{Ext}_{\overline{{\cal O}_{\epsilon}[G]}}^*(k,k)$,
a graded commutative algebra, and, for any finite-dimensional
$\overline{{\cal O}_{\epsilon}[G]}$-module $M$, the
$\mbox{Ext}_{\overline{{\cal O}_{\epsilon}[G]}}^*(k,k)$-module
$\mbox{Ext}_{\overline{{\cal O}_{\epsilon}[G]}}^*(k,M)$.
We prove that for sufficiently large $\ell$ there is
an isomorphism of graded algebras\[
\mbox{Ext}_{\overline{{\cal O}_{\epsilon}[G]}}^*(k,k)
\cong k[X_1,\ldots ,X_{2N}],\]
where each $X_i$ is homogeneous of degree $2$, and
$2N$ equals the number of roots associated to $G$.
Moreover we show that in this case
$\mbox{Ext}_{\overline{{\cal O}_{\epsilon}[G]}}^*(k,M)$is a finitely generated
$\mbox{Ext}_{\overline{{\cal O}_{\epsilon}[G]}}^*(k,k)$-module.
We also show under much less restrictive conditions on
$\ell$ that $\mbox{Ext}_{\overline{{\cal O}_{\epsilon}[G]}}^*(k,k)$
continues to be a finitely generated graded commutative algebra over which
$\mbox{Ext}_{\overline{{\cal O}_{\epsilon}[G]}}^*(k,M)$ is a
finitely generated module.\vspace{6mm}\noindent
1991 Mathematics Subject Classification: 16W30, 17B37, 17B56.

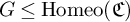
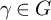
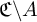
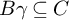
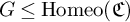
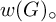
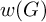
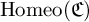
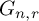
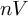
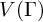
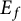
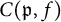
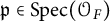
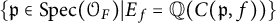
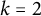
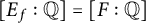
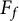
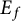
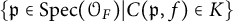
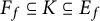
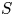
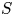
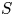
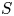
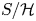
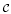 be a finite category and let
be a finite category and let 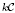 and show that
and show that 