2 results
FINITELY DOMINATED COVERING SPACES OF 3- AND 4-MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 99-108
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
-
If P is a closed 3-manifold the covering space associated to a finitely presentable subgroup ν of infinite index in π1(P) is finitely dominated if and only if P is aspherical or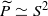
. There is a corresponding result in dimension 4, under further hypotheses on π and ν. In particular, if M is a closed 4-manifold, ν is an ascendant, FP3, finitely-ended subgroup of infinite index in π1(M), π is virtually torsion free and the associated covering space is finitely dominated then either M is aspherical or 
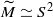or S3. In the aspherical case such an ascendant subgroup is usually Z, a surface group or a PD3-group.
. There is a corresponding result in dimension 4, under further hypotheses on 
or Free Group Actions on Spaces Homotopy Equivalent to a Sphere
-
- Journal:
- Compositio Mathematica / Volume 120 / Issue 3 / February 2000
- Published online by Cambridge University Press:
- 04 December 2007, pp. 327-333
- Print publication:
- February 2000
-
- Article
-
- You have access
- Export citation
