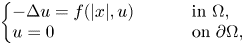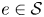1 results
A monotonicity result under symmetry and Morse index constraints in the plane
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 21 July 2020, pp. 885-915
- Print publication:
- June 2021
-
- Article
- Export citation
-
This paper deals with solutions of semilinear elliptic equations of the type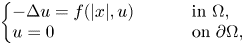
where Ω is a radially symmetric domain of the plane that can be bounded or unbounded. We consider solutions u that are invariant by rotations of a certain angle θ and which have a bound on their Morse index in spaces of functions invariant by these rotations. We can prove that or u is radial, or, else, there exists a direction
\[ \left\{\begin{array}{@{}ll} -\Delta u = f(|x|, u) \qquad & \text{ in } \Omega, \\ u= 0 & \text{ on } \partial \Omega, \end{array} \right. \]
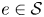$e\in \mathcal {S}$ such that u is symmetric with respect to e and it is strictly monotone in the angular variable in a sector of angle θ/2. The result applies to least-energy and nodal least-energy solutions in spaces of functions invariant by rotations and produces multiplicity results.
