1 results
Rate of strong convergence to Markov-modulated Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 18 January 2022, pp. 1-16
- Print publication:
- March 2022
-
- Article
- Export citation
-
Latouche and Nguyen (2015b) constructed a sequence of stochastic fluid processes and showed that it converges weakly to a Markov-modulated Brownian motion (MMBM). Here, we construct a different sequence of stochastic fluid processes and show that it converges strongly to an MMBM. To the best of our knowledge, this is the first result on strong convergence to a Markov-modulated Brownian motion. Besides implying weak convergence, such a strong approximation constitutes a powerful tool for developing deep results for sophisticated models. Additionally, we prove that the rate of this almost sure convergence is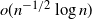
$o(n^{-1/2} \log n)$
. When reduced to the special case of standard Brownian motion, our convergence rate is an improvement over that obtained by a different approximation in Gorostiza and Griego (1980), which is 
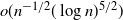$o(n^{-1/2}(\log n)^{5/2})$
.
