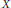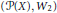1 results
First Variation Formula in Wasserstein Spaces over Compact Alexandrov Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 4 / 01 December 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 723-735
- Print publication:
- 01 December 2012
-
- Article
-
- You have access
- Export citation
-
We extend results proved by the second author (Amer. J. Math., 2009) for nonnegatively curved Alexandrov spaces to general compact Alexandrov spaces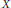
$X$ with curvature bounded below. The gradient flow of a geodesically convex functional on the quadratic Wasserstein space 
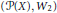$\left( \mathcal{P}\left( X \right),\,{{W}_{2}} \right)$ satisfies the evolution variational inequality. Moreover, the gradient flow enjoys uniqueness and contractivity. These results are obtained by proving a first variation formula for the Wasserstein distance.
