A linear étale representation of a complex algebraic group G is given by a complex algebraic G-module V such that G has a Zariski-open orbit in V and 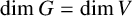$\dim G=\dim V$ . A current line of research investigates which reductive algebraic groups admit such étale representations, with a focus on understanding common features of étale representations. One source of new examples arises from the classification theory of nilpotent orbits in semisimple Lie algebras. We survey what is known about reductive algebraic groups with étale representations and then discuss two classical constructions for nilpotent orbit classifications due to Vinberg and to Bala and Carter. We determine which reductive groups and étale representations arise in these constructions and we work out in detail the relation between these two constructions.