We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper we investigate the motion of a rigid ball in an
incompressible perfect fluid occupying ${\mathbb R}^2$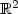
.
We prove the global in time existence and the uniqueness of
the classical solution for this fluid-structure problem. The proof relies
mainly on weighted estimates for the vorticity associated with
the strong solution of a fluid-structure problem
obtained by incorporating some dissipation.
