We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
It is well known that for any integers k and g, there is a graph with chromatic number at least k and girth at least g. In 1960s, Erdös and Hajnal conjectured that for any k and g, there exists a number h(k,g), such that every graph with chromatic number at least h(k,g) contains a subgraph with chromatic number at least k and girth at least g. In 1977, Rödl proved the case when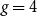 
$g=4$
, for arbitrary k. We prove the fractional chromatic number version of Rödl’s result.
