1 results
A NEW COMPUTATION OF THE Σ-ORDINAL OF KPω
-
- Journal:
- The Journal of Symbolic Logic / Volume 79 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 17 April 2014, pp. 306-324
- Print publication:
- March 2014
-
- Article
- Export citation
-
We define a functional interpretation of KPω using Howard’s primitive recursive tree functionals of finite type and associated terms. We prove that the Σ-ordinal of KPω is the least ordinal not given by a closed term of the ground type of the trees (the Bachmann-Howard ordinal). We also extend KPω to a second-order theory with Δ1-comprehension and strict-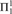
${\rm{\Pi }}_1^1$ reflection and show that the Σ-ordinal of this
theory is still the Bachmann-Howard ordinal. It is also argued that the
second-order theory is Σ1-conservative over
KPω.
