1 results
Girsanov Transformations for Non-Symmetric Diffusions
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 3 / 01 June 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 534-547
- Print publication:
- 01 June 2009
-
- Article
-
- You have access
- Export citation
-
Let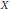
$X$ be a diffusion process, which is assumed to be associated with a (non-symmetric) strongly local Dirichlet form 
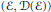$(\varepsilon ,\mathcal{D}(\varepsilon ))$ on 
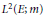${{L}^{2}}(E;m)$. For 
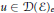$u\,\in \,\mathcal{D}{{(\varepsilon )}_{e}}$, the extended Dirichlet space, we investigate some properties of the Girsanov transformed process 
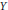$Y$ of 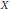$X$. First, let 
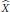$\hat{X}$ be the dual process of 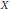$X$ and 
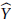$\hat{Y}$ the Girsanov transformed process of 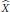$\hat{X} $. We give a necessary and sufficient condition for 
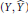$(Y,\hat{Y})$ to be in duality with respect to the measure 
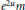${{e}^{2u}}m$. We also construct a counterexample, which shows that this condition may not be satisfied and hence 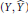$(Y,\hat{Y})$ may not be dual processes. Then we present a sufficient condition under which 
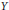$Y$ is associated with a semi-Dirichlet form. Moreover, we give an explicit representation of the semi-Dirichlet form.
