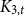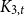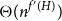The second smallest eigenvalue of the Laplacian matrix, known as algebraic connectivity, determines many network properties. This paper investigates the optimal design of interconnections that maximizes algebraic connectivity in multilayer networks. We identify an upper bound for maximum algebraic connectivity for total weight below a threshold, independent of interconnections pattern, and only attainable with a particular regularity condition. For efficient numerical approaches in regions of no analytical solution, we cast the problem into a convex framework and an equivalent graph embedding problem associated with the optimum diffusion phases in the multilayer. Allowing more general settings for interconnections entails regions of multiple transitions, giving more diverse diffusion phases than the more studied one-toone interconnection case. When there is no restriction on the interconnection pattern, we derive several analytical results characterizing the optimal weights using individual Fiedler vectors. We use the ratio of algebraic connectivity and layer sizes to explain the results. Finally, we study the placement of a limited number of interlinks heuristically, guided by each layer’s Fiedler vector components.

Given a fixed graph H that embeds in a surface $\Sigma$ , what is the maximum number of copies of H in an n-vertex graph G that embeds in $\Sigma$ ? We show that the answer is $\Theta(n^{f(H)})$ , where f(H) is a graph invariant called the ‘flap-number’ of H, which is independent of $\Sigma$ . This simultaneously answers two open problems posed by Eppstein ((1993) J. Graph Theory17(3) 409–416.). The same proof also answers the question for minor-closed classes. That is, if H is a $K_{3,t}$ minor-free graph, then the maximum number of copies of H in an n-vertex $K_{3,t}$ minor-free graph G is $\Theta(n^{f'(H)})$ , where f′(H) is a graph invariant closely related to the flap-number of H. Finally, when H is a complete graph we give more precise answers.

Research on graph representation learning has received great attention in recent years since most data in real-world applications come in the form of graphs. High-dimensional graph data are often in irregular forms. They are more difficult to analyze than image/video/audio data defined on regular lattices. Various graph embedding techniques have been developed to convert the raw graph data into a low-dimensional vector representation while preserving the intrinsic graph properties. In this review, we first explain the graph embedding task and its challenges. Next, we review a wide range of graph embedding techniques with insights. Then, we evaluate several stat-of-the-art methods against small and large data sets and compare their performance. Finally, potential applications and future directions are presented.

This article continues the study of the genus of regular languages that the authors introduced in a 2013 paper (published in 2018). In order to understand further the genus g(L) of a regular language L, we introduce the genus size of |L|gen to be the minimal size of all finite deterministic automata of genus g(L) computing L.We show that the minimal finite deterministic automaton of a regular language can be arbitrarily far away from a finite deterministic automaton realizing the minimal genus and computing the same language, in terms of both the difference of genera and the difference in size. In particular, we show that the genus size |L|gen can grow at least exponentially in size |L|. We conjecture, however, the genus of every regular language to be computable. This conjecture implies in particular that the planarity of a regular language is decidable, a question asked in 1976 by R. V. Book and A. K. Chandra. We prove here the conjecture for a fairly generic class of regular languages having no short cycles. The methods developed for the proof are used to produce new genus-based hierarchies of regular languages and in particular, we show a new family of regular languages on a two-letter alphabet having arbitrary high genus.