1 results
Skew group categories, algebras associated to Cartan matrices and folding of root lattices
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1-45
-
- Article
-
- You have access
- HTML
- Export citation
-
For an action of a finite group on a finite EI quiver, we construct its ‘orbifold’ quotient EI quiver. The free EI category associated to the quotient EI quiver is equivalent to the skew group category with respect to the given group action. Specializing the result to a finite group action on a finite acyclic quiver, we prove that, under reasonable conditions, the skew group category of the path category is equivalent to a finite EI category of Cartan type. If the ground field is of characteristic $p$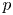
and the acting group is a cyclic $p$
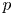-group, we prove that the skew group algebra of the path algebra is Morita equivalent to the algebra associated to a Cartan matrix, defined in [C. Geiss, B. Leclerc, and J. Schröer, Quivers with relations for symmetrizable Cartan matrices I: Foundations, Invent. Math. 209 (2017), 61–158]. We apply the Morita equivalence to construct a categorification of the folding projection between the root lattices with respect to a graph automorphism. In the Dynkin cases, the restriction of the categorification to indecomposable modules corresponds to the folding of positive roots.
