Is there a nontrivial automorphism of the Turing degrees? It is a major open problem of computability theory. Past results have limited how nontrivial automorphisms could possibly be. Here we consider instead how an automorphism might be induced by a function on reals, or even by a function on integers. We show that a permutation of ω cannot induce any nontrivial automorphism of the Turing degrees of members of 2ω, and in fact any permutation that induces the trivial automorphism must be computable.

A main idea of the proof is to consider the members of 2ω to be probabilities, and use statistics: from random outcomes from a distribution we can compute that distribution, but not much more.

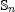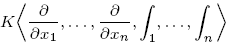
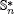The algebra of one-sided inverses of a polynomial algebra Pn in n variables is obtained from Pn by adding commuting left (but not two-sided) inverses of the canonical generators of the algebra Pn. The algebra is isomorphic to the algebra

of scalar integro-differential operators provided that char(K) = 0. Ignoring the non-Noetherian property, the algebra belongs to a family of algebras like the nth Weyl algebra An and the polynomial algebra P2n. Explicit generators are found for the group Gn of automorphisms of the algebra and for the group of units of (both groups are huge). An analogue of the Jacobian homomorphism AutK-alg (Pn) → K* is introduced for the group Gn (notice that the algebra is non-commutative and neither left nor right Noetherian). The polynomial Jacobian homomorphism is unique. Its analogue is also unique for n > 2 but for n = 1, 2 there are exactly two of them. The proof is based on the following theorem that is proved in the paper: