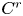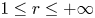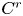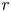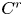1 results
Fast growth of the number of periodic points arising from heterodimensional connections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 02 August 2021, pp. 1899-1963
- Print publication:
- September 2021
-
- Article
- Export citation